Auto-Encoder
定义
定义：Auto-Encoder是一种通过无监督的方式来学习一组数据的有效表示。
形式
形式：原始D维样本->Encoder->M维->Decoder->D维
目标
目标：自编码器的学习 目标是最小化重构误差，即经过Decoder还原的向量与原始向量相差最小。
示意图
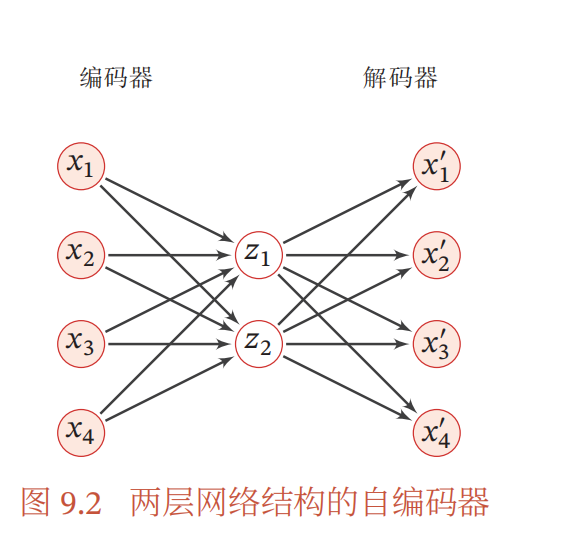
变形
稀疏自编码器
基本的自编码器通常是学习低维的编码，当需要学习的隐藏维度D大于样本的维度，同时希望编码尽可能的稀疏，这就是稀疏自编码器。
堆叠自编码器 两层神经网络的自编码器不足以获得好的数据表示，使用更深的网络以捕获数据的语义信息，这就是堆叠自编码器。
降噪自编码器
原始数据引入噪声，再送入Encoder,让Decoder的输出还原原始输入。
如何引入噪声：输入的数据随机用0进行mask
特点
非监督学习
拥有特征提取能力
使用神经网络对数据进行降维，这是一种非线性的
变分自编码器
VAE 产生了输入数据中不包含的数据，（可以认为产生了含有某种特定信息的新的数据），而 AE 只能产生尽可能接近或者就是以前的数据（当数据简单时，编码解码损耗少时）。
若给定一个数据集，如果我们想要根据这个来生成新的数据。假如我们知道这个分布是什么样，那么我们就可以在这个分布上进行sample进而便可以生成出新的数据。如下图的宝可梦服从\(P(x)\)分布，我们如果知道这个分布便可以进行生成新的数据，但是现在并不知道这个分布啊。
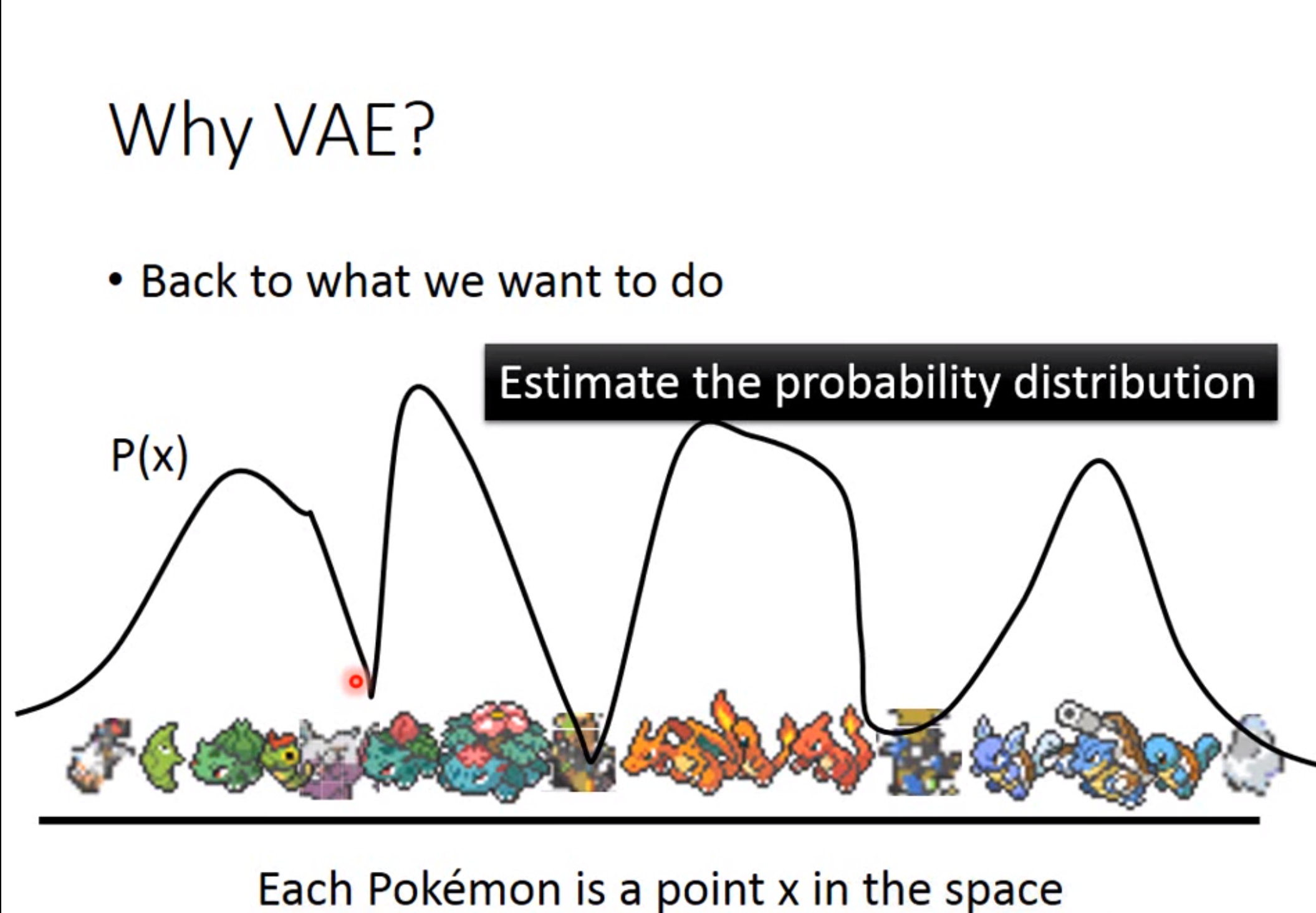
退而求其次，我们如果知道一个隐变量z的分布，将z的分布和数据分布\(P(x)\)进行映射。这样，如果给一个z我们边将其对应到数据分布上即可。即 \[ P(x)=\int_{z}p(z)p(x|z)dz \] 一般假设\(p(z)\)和\(p(x|z)\)是正态分布，只是参数未知，因此可以通过最大似然来进行估计。这一步假设相当于假设隐变量z每个点对应一个高斯分布，z的取值有无穷个，因此数据的分布服从于无穷维的高斯混合分布。
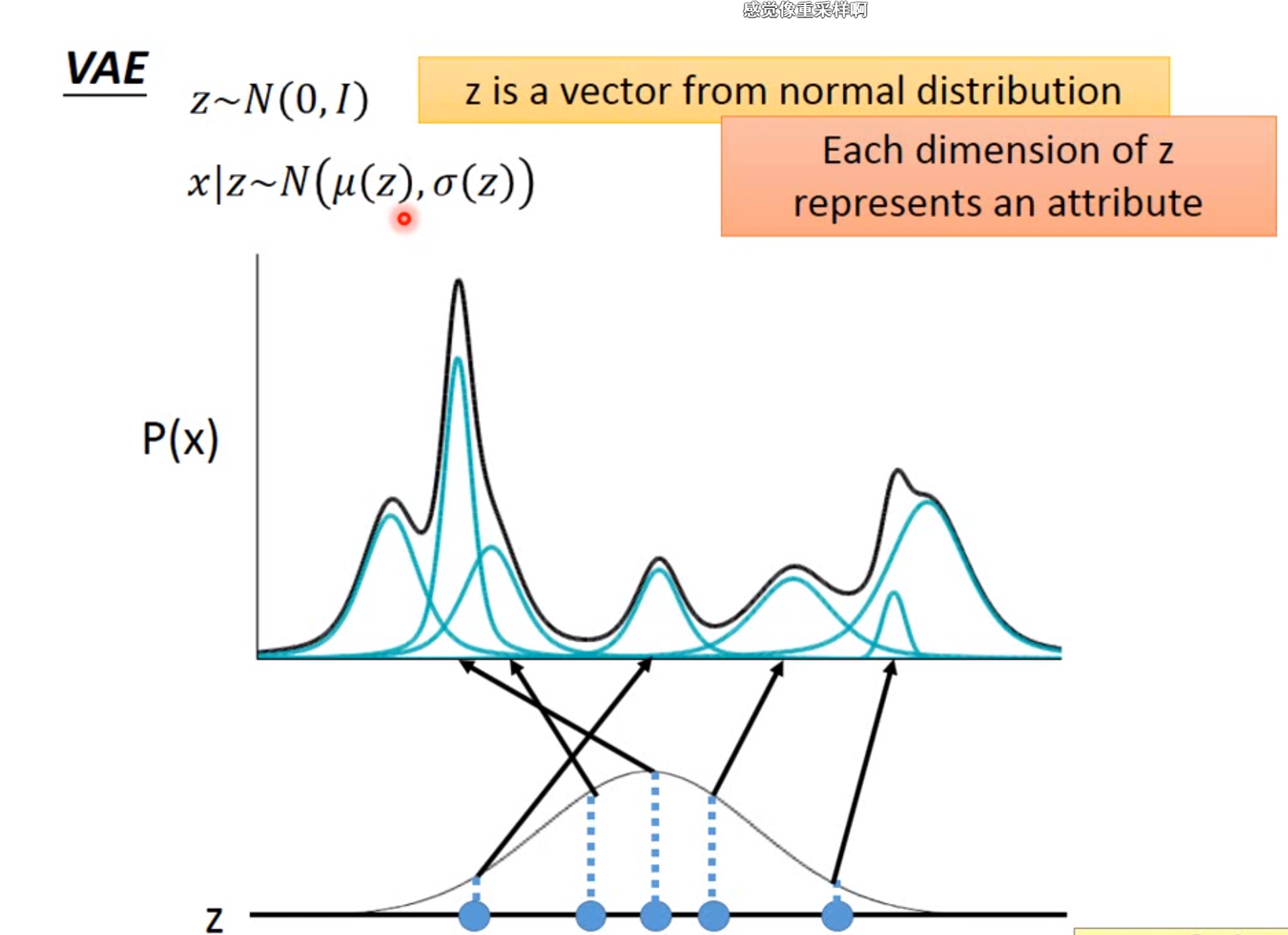
公式推导
\[ logP(x)=log(P(x))\int_zq(z|x)dz=\int_zq(z|x)log(P(x))dz \]
引入一个变分密度函数\(q(z|x)\)可以是任意分布,这一步相当于等价变换 \[ logP(x)=\int_zq(z|x)log{\frac{P(z,x)}{P(z|x)}}dz\\=\int_zq(z|x)log{(\frac{P(z,x)}{q(z|x)} \frac{q(z|x)}{P(z|x)})}dz\\=\int_zq(z|x)log({\frac{P(z,x)}{q(z|X)}})dz+\int_zq(z|x)log(\frac{q(z|x)}{P(z|x)})dz \] 在上式中，因为\(\int_zq(z|x)log(\frac{q(z|x)}{P(z|x)})dz=KL(q(z|x)||P(z|x))\)，因为KL散度衡大于等于0，上式存在下界\(ELBO=L_b=\int_zq(z|x)log({\frac{P(z,x)}{q(z|X)}})dz\)
此时， \[ logP(x)=L_b+KL(q(z|x)||P(z|x))logP(x)=L_b+KL(q(z|x)||P(z|x)) \] 此时最大化对数似然可以使用EM算法来求解：
（1）E步：固定\(P(z|x)\)，使得\(q(z|x)\)尽可能的等于或接近\(P(z|x)\)。使用神经网络调参逼近来将KL=0。也可以理解为让神经网络学习到原始数据和隐变量z的对应关系。
（2）M步：固定\(q(z|x)\)使得EMLO最大。
\[
ELBO=\int_zq(z|x)log(\frac{P(x|z)P(z)}{q(z|x)})dz\\=\int_zq(z|x)log(\frac{p(z)}{q(z|x)})dz+\int_zq(z|x)log(p(x|z))dz\\=-KL(q(z|x)||p(z))+E_{q(z|x)}log(P(x|z))
\] 因此最大化ELBO等价于，最小化第一项（Encoder），最大化第二项（Decoder）。最小化第一项：让\(q(z|x)\)分布和\(p(z)\)分布越近越好，因为假设\(p(z)\)分从正态分布，这便相当于让\(q(z|x)\)和正态分布越近越好。这一步相当于，对编码器输出的分布进行约束。
最大化第二项：相当于通过x采样到的隐变量z，用z还原x与原始的x相近。这一步相当于使得重构误差最小。!
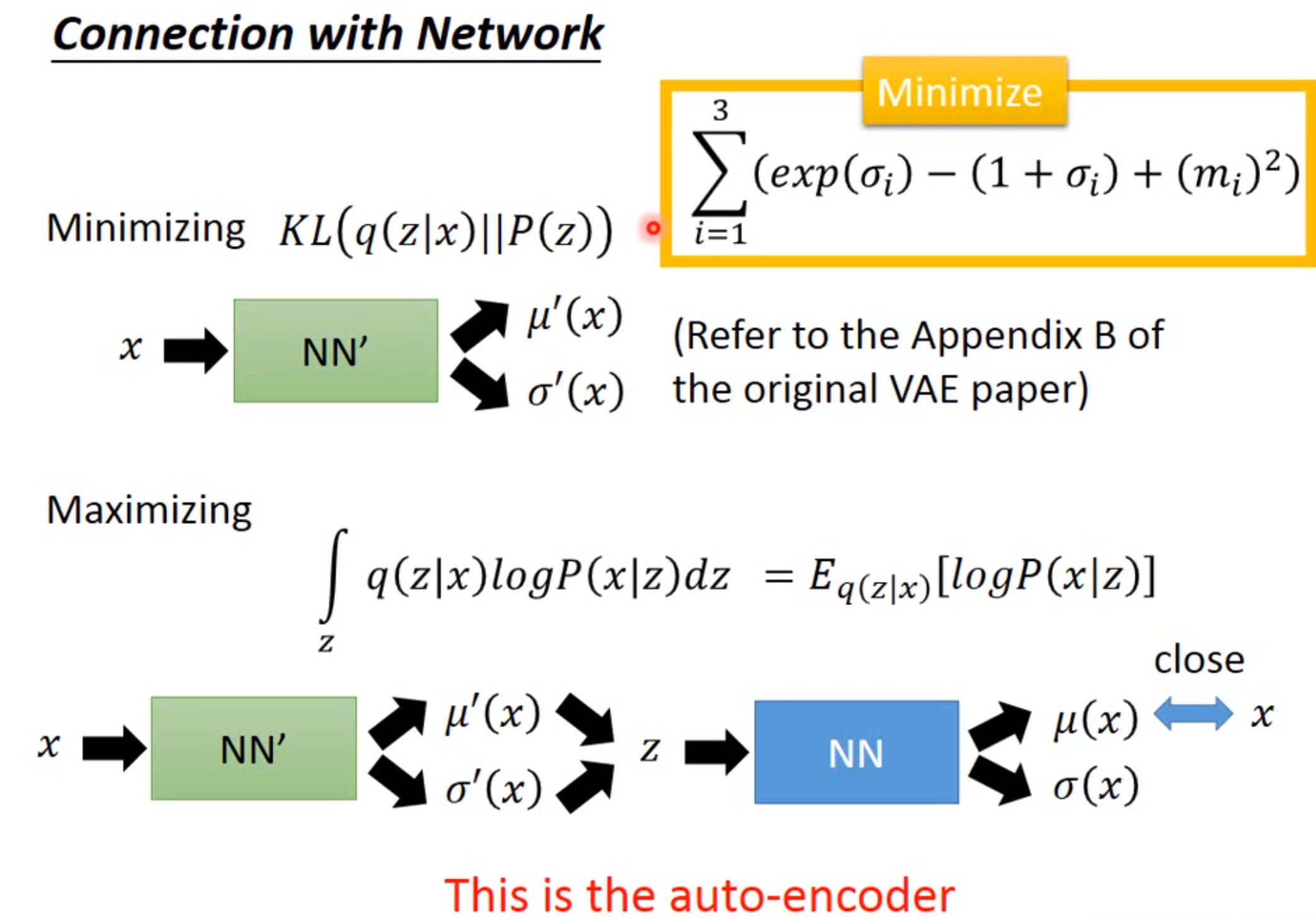
本质
VAE的本质相当于为每个样本构造专属的均值和方差，然后重构采样。\(P(x)=\int_{z}p(z)p(x|z)dz\)相当于先确定隐变量z属于哪类样本，然后根据这类的样本生成一个新的x。这种方法显式的估计了数据分布的密度函数。
与GAN的区别
- 区别1：loss不同。VAE的loss是pointwise loss即重构损失，对比重构的X和原始输入X的差距，虽然也有KL散度，但是本质是让encoder的输出尽可能与正态分布相近。GAN的loss是衡量分布之间的loss，GAN的loss可以转换为JS散度。
- 区别2：是否为显式的概率密度函数。VAE中神经网络只是用来拟合假定的分布，这样限制了神经网络的能力。GAN中低维的正态分布P(z)，直接用神经网络学习一个映射函数\(G:z\rightarrow x\)，这个映射函数便是生成器。
函数，这个映射函数便是生成器。